小学奥数-巧算求三角形面积公式

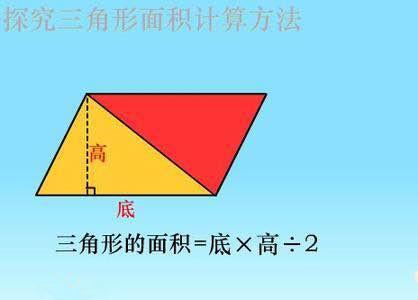
三角形面积的计算公式：底×高÷2，

1.三角形求面积时，常用到以下几点：

（1）两个三角形的高相等，则他们的面积比等于对应底边的比；

（2）两个三角形的底边相等，则它们的面积比等于对应高的比；

（3）蝴蝶模型：梯形的上、下底和对角线组成的两个相似三角形对应边的比相等。

2.特殊三角形的特征：

（1）等边三角形，三个内角均为60°； （2）等腰三角形两个底角相等；

（3）等腰直角三角形常和正方形联系在一起。

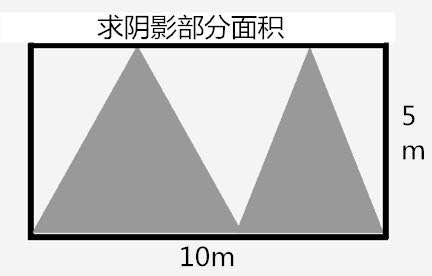
精讲1：下图是两个相同的三角形叠在一起，求阴影部分的面积。（单位：厘米）

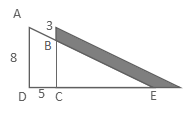
分析：运用转化的思想，将无法求得的面积转化为规则图形。由题意可知，阴影部分的面积等于梯形ABCD的面积。梯形的下底为8厘米，上底可以求出（8-3）厘米，高为5厘米，运用梯形面积公式：（上底+下底）×高÷2，可求出。

解: [8+（8-3）]×5÷2=13×5÷2=32.5（平方厘米）

答:阴影部分的面积是32.5平方厘米。

精讲2：大正方形边长5厘米，小正方形边长3厘米，求图中的阴影部分的面积。

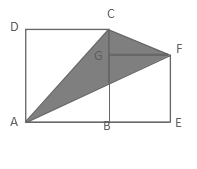
分析：观察上图可知，阴影部分的面积=大正方形的面积+小正方形的面积-三角形ACD的面积-三角形AEF的面积+三角形CFG的面积。大正方形的面积=5×5=25平方厘米，小正方形的面积=3×3=9平方厘米，三角形ACD的面积=5×5÷2=12.5平方厘米，三角形AEF的面积=3×（5+3）÷2=12平方厘米，三角形CFG的面积=（5-3）×3÷2=3平方厘米。

解：5×5+3×3-5×5÷2-3×（5+3）÷2+（5-3）×3÷2

=25+9-12.5-12+3

=12.5（平方厘米）

答：阴影部分的面积是12.5平方厘米。

精讲3：.如图中，梯形ABCD上底AD=16厘米，高BD=21厘米，并且BD=3DE，则△ADE的面积是多少平方厘米？梯形下底BC长多少厘米？

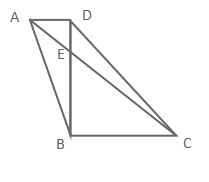
解：DE=7, S△ADE=16×7÷2=56 ,由蝴蝶模型，AD:BC=DE:BE=1:2, BC=32

答：△ADE的面积是56平方厘米；梯形下底BC长32厘米。

精讲4：如图所示，D、E、F分别是BC、AD、BE的三等分点，△ABC的面积等于27平方厘米，求△DEF的面积。

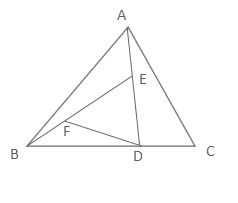
分析：由题意可知，D是BC的三等分点，则BD=2/3BC,△ABD和△ABC同高，那么S△ABD= 2/3S△ABC。同理可以推出S△BDE= 2/3S△ABD，S△DEF= 2/3 S△BDE。

解：S△ABD= 2/3×27=18（平方厘米）

S△BDE= 2/3 ×18=12（平方厘米）

S△DEF= 2/3 ×12=8（平方厘米）

答：△DEF的面积是8平方厘米。

精讲5：如图所示，已知正方形ABCD的边长是12厘米，E是CD边上的中点，连接对角线AC，交BE于点O，则△AOB的面积是多少平方厘米？

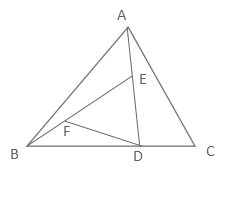
解：由蝴蝶模型知：CO：AO=EC：AB=1:2

因为S正方形ABCD=144平方厘米，

所以S△ABC=72平方厘米；

因为△ABO和△BOC的高相等，所以面积比就等于底边的比=AO:CO=2:1，

所以S△ABO=48平方厘米

答： △ AOB的面积是48平方厘米。